برای شناخت هندسه های نااقلیدسی، ابتدا لازم است با هندسه اقلیدسی که مبتنی بر پنج اصل می باشد (اصل یا بدیهیات آنچنانکه در فلسفه کلاسیک تعریف شدهاست، گزارهای است که پرواضح یا بدیهی است و بدون اینکه بحث یا سؤالی در مورد آن مطرح باشد، مورد پذیرش است) آشنا شد.
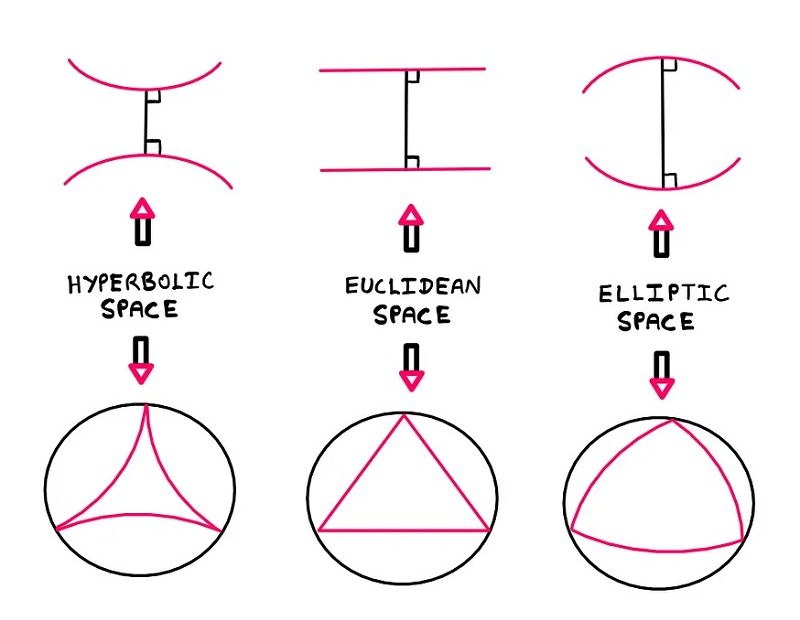
هندسه اقلیدسی
هندسه اقلیدسی دستگاهی ریاضیاتی است که آن را به اقلیدس، ریاضیدان یونانی اهل اسکندریه نسبت میدهند؛ چرا که او در کتاب هندسه خود به نام اصول اقلیدس این نوع هندسه را توصیف نمود. روش اقلیدس شامل فرض گرفتن دسته کوچکی از اصول موضوعههای شهودی، و استنتاج گزارههای زیادی از این اصول میباشد. گرچه که بسیاری از نتایج اقلیدس توسط ریاضیدانان قبل تر از او هم بیان شده بودند، اقلیدس اولین کسی بود که نشان داد چگونه میتوان این گزارهها را در یک دستگاه استنتاجی و منطقی جامع گنجاند.
اصل اول – از هر نقطه می توان خط مستقیمی به هر نقطه ی دیگر کشید.
اصل دوم – هر پاره خط مستقیم را می توان روی همان خط به طور نامحدود امتداد داد.
اصل سوم – می توان دایره ای با هر نقطه دلخواه به عنوان مرکز آن و با شعاعی مساوی هر پاره خط رسم کرد.
اصل چهارم – همه ی زوایای قائمه با هم مساوی اند.
اصل پنجم – از یک نقطه خارج یک خط، یک خط و و تنها یک خط می توان موازی با خط مفروض رسم کرد.
اصل پنجم اقلیدس که ایجاز سایر اصول را نداشت، به هیچ وجه واجد صفت بدیهی نبود. در واقع این اصل بیشتر به یک قضیه شباهت داشت تا به یک اصل! بنابراین طبیعی بود که لزوم واقعی آن به عنوان یک اصل مورد سئوال قرار گیرد. زیرا چنین تصور می شد که شاید بتوان آن را به عنوان یک قضیه نه اصل از سایر اصول استخراج کرد، یا حداقل به جای آن می توان معادل قابل قبول تری قرار داد.
هندسه های هذلولوی
هندسه های هذلولوی توسط بويوئی و لباچفسكی بطور مستقل و همزمان كشف گرديد.
اصل توازی هندسه هذلولوی: از يك خط و يك نقطه ناواقع بر آن دست كم دو خط موازی با خط مفروض می توان رسم كرد.
تمام خطوط غیر متقاطع دیگر دارای یک نقطه حداقل فاصله هستند و از دو طرف آن نقطه واگرا می شوند و به آنها فوق موازی، موازی واگرا یا گاهی اوقات غیر متقاطع می گویند. برخی از هندسهسنجها به سادگی از عبارت «خطوط موازی» به معنای «محدود کردن خطوط موازی» استفاده میکنند، در حالی که خطوط فوق موازی به معنای غیر متقاطع هستند.
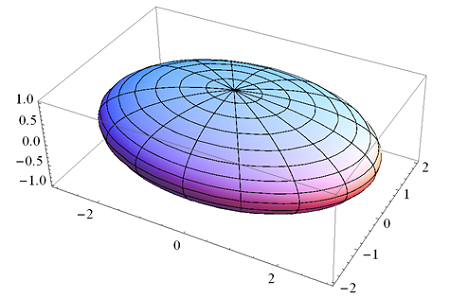
هندسه های بیضوی
در سال ۱۸۵۴ برنارد ریمان نشان داد که اگر نامتناهی بودن خط مستقیم کنار گذاشته شود و صرفاً بی کرانگی آن مورد پذیرش واقع شود، آنگاه با چند جرح و تعدیل جزیی اصول موضوعه دیگر، هندسه سازگار نااقلیدسی دیگری را می توان به دست آورد. پس از این تغییرات اصل توازی هندسه بیضوی بصورت زیر ارایه گردید.
اصل توازی هندسه بیضوی – از یک نقطه ناواقع بر یک خط نمی توان خطی به موازات خط مفروض رسم کرد.
در هندسه بیضوی، دو خط عمود بر یک خط معین باید قطع شوند. در واقع، عمودهای یک طرف همگی در یک نقطه به نام قطب مطلق آن خط قطع می شوند. عمودهای طرف دیگر نیز در یک نقطه قطع می شوند. با این حال، برخلاف هندسه کروی، قطب های دو طرف یکسان هستند. این به این دلیل است که در هندسه بیضوی هیچ نقطه پادپایی وجود ندارد. به عنوان مثال، این امر در مدل ابرکروی با ساختن “نقاط” در هندسه ما در واقع جفت نقاط متضاد روی یک کره به دست می آید. دلیل انجام این کار این است که به هندسه بیضوی اجازه می دهد این اصل را برآورده کند که یک خط منحصر به فرد از هر دو نقطه عبور می کند.
در هندسه اقلیدسی، یک شکل می تواند به طور نامحدود بزرگ یا کوچک شود، و ارقام حاصل شبیه به هم هستند، یعنی دارای زوایای یکسان و نسبت های داخلی یکسان هستند. در هندسه بیضوی اینطور نیست. به عنوان مثال، در مدل کروی می بینیم که فاصله بین هر دو نقطه باید کاملاً کمتر از نصف محیط کره باشد، زیرا نقاط پادپایی مشخص هستند.

کاربرد
هندسه غیر اقلیدسی کاربرد قابل توجهی در دنیای علمی دارد. مفهوم هندسه غیر اقلیدسی در کیهان شناسی برای مطالعه ساختار، مبدأ و ساختار و تکامل جهان به کار می رود. هندسه غیر اقلیدسی برای بیان نظریه نسبیت، جایی که فضا منحنی است، استفاده می شود. اندازه گیری فواصل، مساحت ها، زوایای نقاط مختلف زمین با کمک هندسه غیر اقلیدسی انجام می شود. همچنین هندسه غیر اقلیدسی در مکانیک سماوی کاربرد دارد.
گسترش
هندسه نئو اقلیدسی بعدها توسط گاوس و ریمان در قالب یک هندسه کلی تر توسعه یافت. این هندسه عمومی تری است که در نظریه نسبیت عام انیشتین استفاده شده است. در هندسه غیر اقلیدسی، مجموعه زوایای داخلی مانند 180 درجه نیست. به عنوان مثال، اگر اضلاع مثلث هذلولی باشد، مجموعه زوایای داخلی هرگز به 180 درجه نمی رسد و کمتر است. همچنین، اگر هندسه بیضوی باشد، هرگز 180 درجه نخواهد بود. بلکه بیشتر است.